Bienvenido al curso sobre Valor absoluto.
El valor absoluto o módulo de un número real ‘x’ se representa por |x| y es el valor no negativo de ‘x’, sin importar su signo, sea este positivo o negativo.
El valor absoluto está vinculado con las nociones de magnitud, distancia y norma en diferentes contextos matemáticos y físicos.
El valor absoluto nor permite relacionar las distancias entre dos puntos sobre la recta real con el concepto de vecindad alrededor de un punto, algo que será muy útil más adelante en la definición del límite de una variable real.
Definición
El valor absoluto de ‘x’ es siempre un número positivo o cero, pero nunca un número negativo. Si ‘x’ es un número negativo, entonces su valor absoluto es necesariamente positivo. Es decir,
![]()
O expresado de otra forma:
![]()
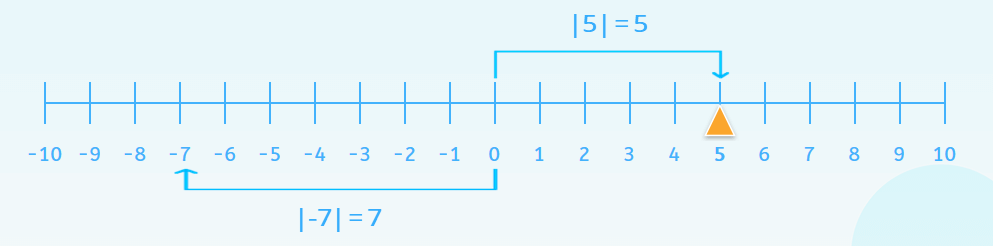
Desde un punto de vista geométrico, el valor absoluto de un número real puede verse como la distancia que existe entre ese número y el cero. De manera general, el valor absoluto de la diferencia entre dos números es la distancia entre ellos.
Así, por ejemplo, el valor absoluto de 5 o el valor absoluto de -7 es en ambos casos la distancia de dichos números al cero.
Definición equivalente
Si ‘x’ es un número real, su valor absoluto es un número real no negativo definido de la siguiente manera:
![]()
Propiedades
Otras propiedades
Ejemplos
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()

![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()