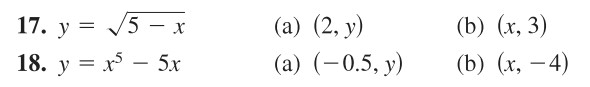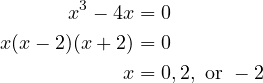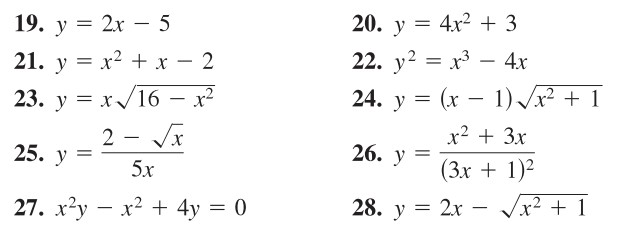Summary
- Sketch the graph of an equation
- Find the intercepts
- Test a graph for simetry with respect to an axis and the origin
- Find the points of intersection of two graphs
- Interpret mathematical models for real life-data
The Graph of an Equation
 In 1637 the French mathematician René Descartes revolutionized the study of mathematics by joining its two major fields: algebra and geometry. With Descarte’s coordinate plane, geometric concepts could be formulated analytically and algebraic concepts could be viewed graphically. The power of this approach was such that with within a century of its introduction, much of the calculus had been developed.
In 1637 the French mathematician René Descartes revolutionized the study of mathematics by joining its two major fields: algebra and geometry. With Descarte’s coordinate plane, geometric concepts could be formulated analytically and algebraic concepts could be viewed graphically. The power of this approach was such that with within a century of its introduction, much of the calculus had been developed.
The same approach can be followed in your study of calculus. That is, by viewing calculus from multiple perspectives -graphically, analytically and numerically- you will increase your understanding of core concepts.
Consider the equation ![]() . The point
. The point ![]() is a solution point of the equation because the equation is satisfied (is true) when
is a solution point of the equation because the equation is satisfied (is true) when ![]() is substituted for
is substituted for ![]() and
and ![]() is substituted for
is substituted for ![]() . This equation has many other solutions, such as
. This equation has many other solutions, such as ![]() and
and ![]() . To find other solutions systematically, solve the original equation for
. To find other solutions systematically, solve the original equation for ![]() .
.
![]()
Then construct a table of values by substituting several values of ![]() .
.
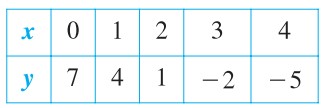
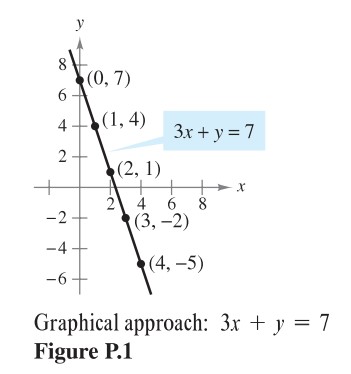
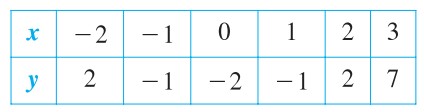
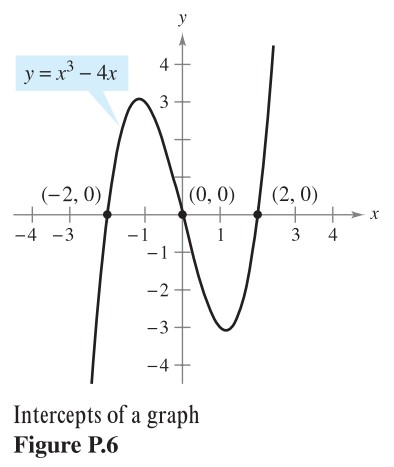
From the table, you can see that ![]() are solutions of the original equation
are solutions of the original equation ![]() . Like many equations, this equation has an infinite nuber of solutions. The sets of all solution point is the graph of the equation, as shown in Figure P1.
. Like many equations, this equation has an infinite nuber of solutions. The sets of all solution point is the graph of the equation, as shown in Figure P1.
Even thought we refer the sketch shown in Figure P1 as the graph of ![]() , it really represents only a portion of the graph. The entire graph would extend beyond this page.
, it really represents only a portion of the graph. The entire graph would extend beyond this page.
In this course, you will study many sketching techniques. The simplest is point plotting. That is, you plot points until the basic shape of the graph seems apparent.
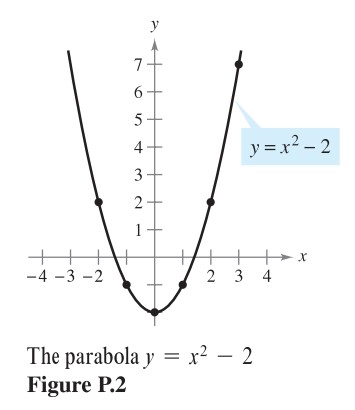
EXAMPLE 1 – Sketching a Graph by Point Plotting |
| Sketch the graph of SolutionFirst construct the table of values. |
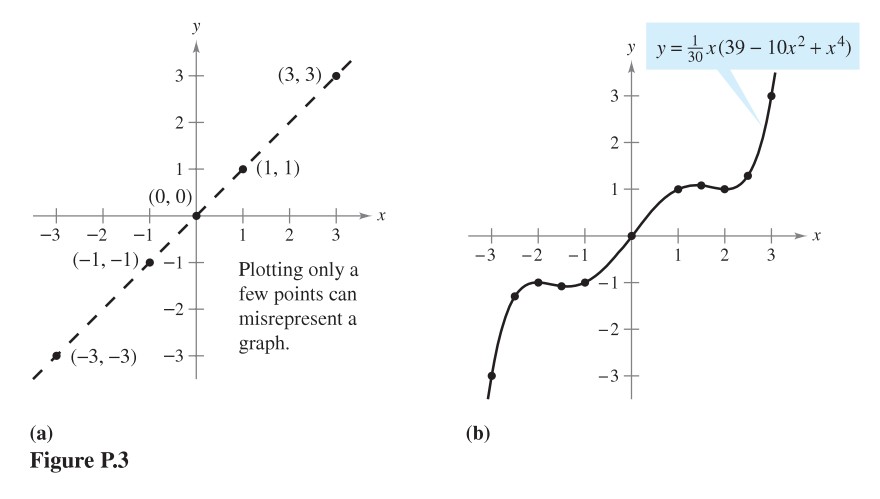
One disadvantage of plotting is that to get a good idea about the shape of a graph, you may need to plot many points. With only a few points, you could badly misrepresent the graph. For instance, suppose that to sketch the graph of
![]()
you plotted only five points: ![]() , as shown in Figure P3 (a). From these five points, you might conclude that the graph is line. This, however, is not correct. By plotting several more points, you can see that the graph is more complicated, as shown in Figure P3 (b).
, as shown in Figure P3 (a). From these five points, you might conclude that the graph is line. This, however, is not correct. By plotting several more points, you can see that the graph is more complicated, as shown in Figure P3 (b).
EXERCISES |
In exercises 1-4, match the equation with its graph. The graphs are labeled (a), (b), (c), and (d).
|
In exercises 5-14, sketch the graph of the equation by point plotting.
|
In exercises 17 and 18, use Geogebra to graph the equation. Find the unknown coordinate of each solution point accurate to two decimal places.
|
Intercepts of a Graph
Two types of solution points that are specially useful in graphing an equation are those having zero as ![]() – or
– or ![]() -coordinate. Such points are called intercepts because they are the points at which the graph intersects the
-coordinate. Such points are called intercepts because they are the points at which the graph intersects the ![]() – or
– or ![]() -axis.
-axis.
The point ![]() is an x-intercept of the graph of an equation if it is a solution point of the equation. To find the
is an x-intercept of the graph of an equation if it is a solution point of the equation. To find the ![]() – intercepts of a graph, let
– intercepts of a graph, let ![]() be zero and solve the equation for
be zero and solve the equation for ![]() .
.
The point ![]() is a y-intercept of the graph of an equation if it is a solution point of the equation. To find the
is a y-intercept of the graph of an equation if it is a solution point of the equation. To find the ![]() -intercepts of a graph, let
-intercepts of a graph, let ![]() be zero and solve the equation for
be zero and solve the equation for ![]() .
.
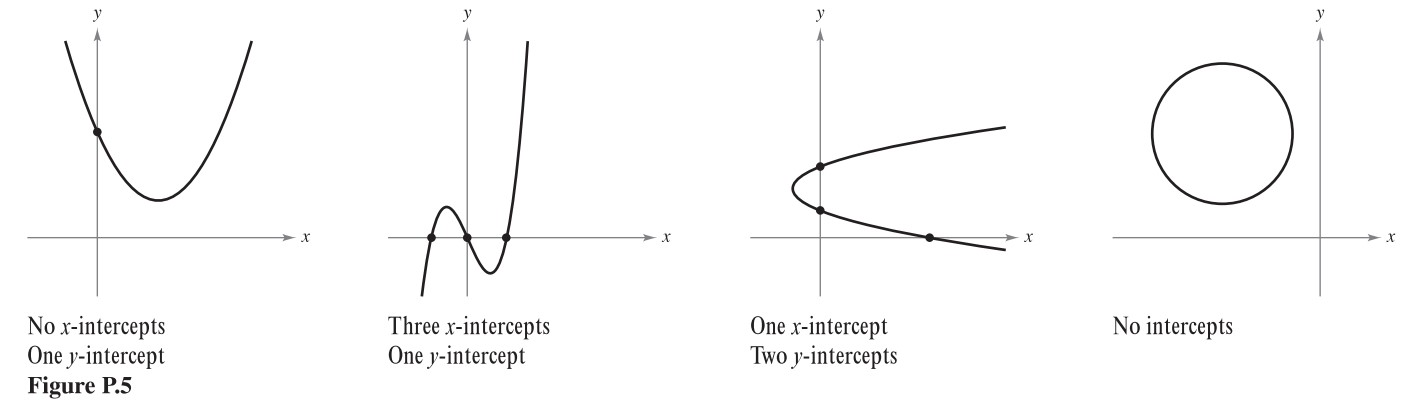
It is possible for a graph to have no intercepts, or it might have several. For instance, consider the graphs shown in Figure P5.
EXAMPLE 2 – Finding x– and y-intercepts |
| Find the SolutionTo find the
Because this equation has three solutions, you can conclude that the graph has three
To find the Doing this proces
|
Example 2 uses an analytic approach to finding intercepts. When an analytic approach is not possible, you can use a graphical approach by finding the points at wich the graph intersects the axes. Use a graphing utility to approximate the intercepts.
EXERCISES |
In Exercises 19-28, find any intercepts.
|
Los