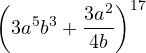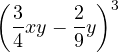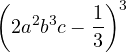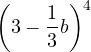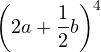Como aplicación de las propiedades de los números combinatorios, podemos escribir el siguiente triángulo aritmético conocido con el nombre de Triángulo de Tartaglia.
![]()
![]()
![]()
![]()
![]()
![]()
![]()
Una vez se desarrollan los números combinatorios, resulta lo siguiente:
![]()
![]()
![]()
![]()
![]()
![]()
![]()
Binomio de Newton
Para multiplicar un polinomio por un monomio, se multiplica cada término del polinomio por cada término del binomio y se reducen los términos semejantes.
Esta regla permite encontrar las potencias de un binomio según el siguiente desarrollo:
![]()
![]()
![]()
![]()
![]()
![]()
En este triángulo observamos que:
- Los exponentes de las potencias de
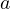 van decreciendo, de unidad en unidad.
van decreciendo, de unidad en unidad. - Los exponentes de las potencias de
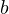 van decreciendo, de unidad en unidad.
van decreciendo, de unidad en unidad. - Los coeficientes de cada término, excepto el primero y el último que son la unidad, se encuentran sumando los coeficientes de los dos términos que hay encima de él, en la fila inmediata superior. Esto justifica que los coeficientes coincidan con los correspondientes números del triángulo de Tartaglia.
Con todo esto, podemos decir que:
|
Ests fórmula es conocida con el nombre de binomio de Newton.
El término ![]() se llama término general y ocupa el lugar
se llama término general y ocupa el lugar ![]() en el desarrollo del binomio. Mediante él podemos obtener sucesivamente todos los términos del desarrollo, atribuyendo a
en el desarrollo del binomio. Mediante él podemos obtener sucesivamente todos los términos del desarrollo, atribuyendo a ![]() los valores 0, 1, 2, 3, …
los valores 0, 1, 2, 3, … ![]() .
.
|
Como podemos observar, se van alternando los signos positivos y negativos.
Ejemplos
![]()
![]()
![]()
![]()
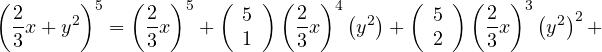
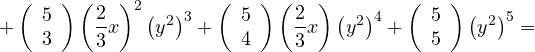
![]()
Observaciones
- Cuando los monomios presentan dificultades, conviene resolver el desarrollo siguiendo estrictamente la regla, haciendo después las operaciones.
- Como los números combinatorios entran en el desarrollo de la potencia de un binomio, reciben también el nombre de coeficientes binómicos.
Ejercicios
Estos ejercicios deben ser resueltos por cada alumno en su libreta. Una vez terminados, se hacen fotos a las páginas donde están sus desarrollos y se envían finalmente a la carpeta ‘Binomio de Newton’ que está enlazada en el botón naranja inferior. Buscar allí dentro una carpeta con el nombre del profesor, acceder a su interior y subir las fotos de esos ejercicios en formato JPG.
El nombre de las fotos deberá tener el siguiente formato:
apellido1-apellido2-nombre-numero_imagen.jpg
Más ejercicios
Igualmente, resolver estos ejercicios en la libreta y subir las fotos en formato JPG a la carpeta correspondiente del profesor, dentro de la carpeta ‘Binomio de Newton’.
El nombre de las fotos deberá tener el siguiente formato:
apellido1-apellido2-nombre-numero_imagen.jpg
1. Encontrar el cuarto término de la potencia ![]()
2. Encontrar el octavo término del desarrollo de la potencia ![]()
3. Encontrar el término que contiene ![]() en el desarrollo de la potencia
en el desarrollo de la potencia ![]()
4. Escribe el término que contiene ![]() en el desarrollo de la potencia
en el desarrollo de la potencia ![]()
5. Encontrar el término que contiene ![]() en el desarrollo de la potencia
en el desarrollo de la potencia 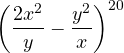
6. Encontrar el término que contiene ![]() en el desarrollo de la potencia
en el desarrollo de la potencia