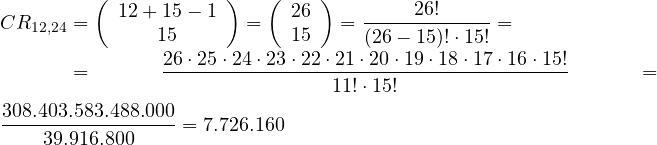Las combinaciones con repetición de ![]() elementos tomados de
elementos tomados de ![]() en
en ![]() son los distintos grupos de
son los distintos grupos de ![]() elementos iguales o distintos que se pueden hacer con los
elementos iguales o distintos que se pueden hacer con los ![]() elementos que tenemos, de forma que dos grupos se diferencian en algún elemento y no en el orden de colocación. Se representa por
elementos que tenemos, de forma que dos grupos se diferencian en algún elemento y no en el orden de colocación. Se representa por ![]() .
.
Para construir las variaciones con repetición, partimos de un conjunto ![]() y elaboramos todas las variaciones con repetición posibles.
y elaboramos todas las variaciones con repetición posibles.
De un elemento: Si tenemos un conjunto de tres elementos y queremos hacer grupos de uno, únicamente podremos hacer cuatro grupos:
1, 2, 3, 4
De dos elementos: La forma de construirlas será similar a las combinaciones sin repetición aunque con la diferencia de que al permitirse repetir los elementos tendremos que añadir a cada una de las de orden uno, el mismo elemento y todos los siguientes. Obsérvese cómo se van eliminando los elementos repetidos (21, 31, 32, 41, 42, 43) pues el orden no importa.
Así se obtienen los pares:
11, 12, 13, 14
22, 23, 24
33, 34,
44
De tres elementos: Se pueden construir a partir de las anteriores, añadiendo a cada combinación de orden dos el último elemento y todos los elementos siguientes. Obsérvese nuevamente cómo se eliminan los elementos repetidos pero con diferente orden en los números.
Se obtienen las siguientes ternas:
111, 112, 113, 114, 122, 123, 124, 133, 134, 144
222, 223, 224, 233, 234, 244
333, 334, 344
444
De cuatro elementos: Se pueden obtener a partir de las de orden tres, añadiendo a cada una de ellas el último elemento y los elementos siguientes.
Siguiendo la construcción ordenada que se ha realizado, se puede observar que:
Entonces, ¿cuántas combinaciones con repetición hay?
- De orden uno:
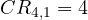
- De orden dos:
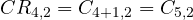
- De orden tres:
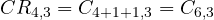
- De orden cuatro:
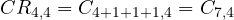
A partir de estas fórmulas es fácil deducir la siguiente fórmula para calcular el número de combinaciones con repetición ![]() .
.
|
Ejemplos
¿Cuántas combinaciones con repetición de 5 elementos tomados de 3 en 3 hay?
ROE – n = 5, r = 3
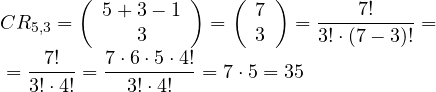
¿Cuántas fichas tiene el juego del dominó?
Una ficha de dominó es un rectángulo dividido en dos partes. En cada una de ellas hay una serie de puntos que indican su valor. Estas puntuaciones van de blanca (cero) hasta 6. Las puntuaciones se representan por pares, pues las fichas tienen dos partes.
ROE – n = 7, r = 2
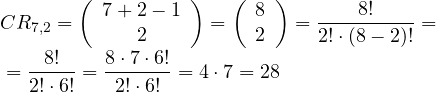
¿De cuántas formas se pueden elegir 4 botellas, si en una bodega hay 5 tipos diferentes de botellas?
ROE – n = 5, r = 4
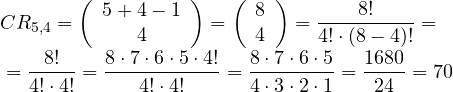
En estos últimos cuatro ejemplos vamos a ver lo que supone el orden, en la medida que diferencia las variaciones de las permutaciones.
En una clase de 10 alumnos se van a repartir 3 premios. ¿De cuántas formas puede hacerse si los premios son diferentes y cada alumno solo puede recibir un premio?
ROE – n = 10, r = 3
![]()
En una clase de 10 alumnos se van a repartir 3 premios. ¿De cuántas formas puede hacerse si los premios son iguales y cada alumno solo puede recibir un premio?
ROE – n = 10, r = 3
![]()
En una clase de 10 alumnos se van a repartir 3 premios. ¿De cuántas formas puede hacerse si los premios son diferentes y cada alumno puede recibir más de un premio?
ROE – n = 10, r = 3
![]()
En una clase de 10 alumnos se van a repartir 3 premios. ¿De cuántas formas puede hacerse si los premios son iguales y cada alumno puede recibir más de un premio?
ROE – n = 10, r = 3
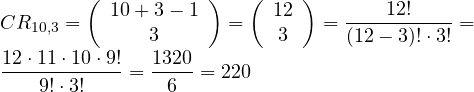
En este vídeo se explica la fórmula más algunos ejemplos sencillos