Combinaciones: Sorteos

 

Q1. Cuántas jugadas diferentes se pueden obtener si se sacan 5 cartas de una baraja de 40 cartas

ROE – n = 40, r = 5

    \[ C_{40,5} = \frac{40!}{5! \cdot (40-5)!} = \frac{40 \cdot 39 \cdot 38 \cdot 37 \cdot 36 \cdot 35!}{5! \cdot 35!} = \frac{78.960.960}{120} = 658.008 \]

Q2. ¿De cuántas formas diferentes se pueden presentar 4 cartas de una baraja, sbiendo que hay 4 ases, 3 reyes, 2 caballos y una sota?

Hay 4A, 3R, 2C y 1S = 10 cartas. No hay repetición y no importa el orden en que se saquen las cartas.

    \[ C_{10,4} = \frac{10!}{4! \cdot (10-4)!} = \frac{10 \cdot 9 \cdot 8 \cdot 7 \cdot 6!}{4! \cdot 6!} = \frac{5040}{24} = 210 \]

Q3. ¿De cuántas formas se pueden extraer 2 bolas rojas y 3 verdes de una urna que contiene 15 bolas rojas y 12 verdes?

En este ejercicio hay que separar las combinaciones en función de los colores de las bolas.

\displaystyle C_{15,2} = \frac{15!}{2! \cdot (15-2)!} = \frac{15 \cdot 14 \cdot 13!}{2! \cdot 13!} = \frac{210}{2} = 105

\displaystyle C_{12,3} = \frac{12!}{3! \cdot (12-3)!} = \frac{12 \cdot 11 \cdot 10 \cdot 9!}{3! \cdot 9!} = \frac{1320}{6} = 220

\displaystyle C_{15,2} \cdot C_{12,3} = 105 \cdot 220 = 23.100

Q4. Cuántas quinielas de 14 resultados hay que sellar para estar seguro de obtener 14 aciertos si se marcan 8 'unos', cuatro 'x' y dos 'doses'
\displaystyle C_{14,8} \cdot C_{6,4} \cdot C_{2,2} = \frac{14!}{8! \cdot (14-8)!} \cdot \frac{6!}{4! \cdot (6-4)!} \cdot \frac{2!}{2! \cdot (2-2)!} = \medskip \\ \displaystyle = \frac{14 \cdot 13 \cdot 12 \cdot 11 \cdot 10 \cdot 9 \cdot 8!}{8! \cdot 6!} \cdot \frac{6 \cdot 5 \cdot 4!}{4! \cdot 2!} \cdot 1 = \frac{2.162.160}{720} \cdot \frac{30}{2} \cdot 1 = \medskip \\ \displaystyle =3.003 \cdot 15 = 45045
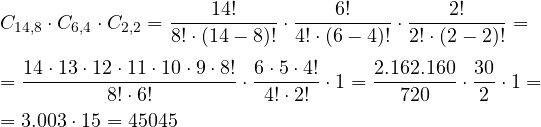
Q5. Cuántas quinielas de 14 resultados hay que sellar para estar seguro de obtener 14 aciertos si hay 5 resultados fijos

ROE – n = 3, r = 9

    \[ VR_{3,9} = 3^9 = 19.683 \]

En el ejercicio anterior no importaba el orden, pues las elecciones (1, X, 2) ya estaban hechas. Pero en este ejercicio no lo están y además hay 5 resultados que están fijados. Luego solo se pueden elegir los resultados de 9 partidos. Importante advertir que en este caso hay repetición, como ya se vio en los ejercicios de variaciones con repetición.

Q6. Cuántas quinielas de 14 resultados hay que sellar para estar seguro de obtener 14 aciertos si se marcan 9 'unos'

\displaystyle C_{14,9} \cdot VR_{2,5} = \frac{14!}{9! \cdot (14-9)!} \cdot 2^5 = \frac{14 \cdot 13 \cdot 12 \cdot 11 \cdot 10 \cdot 9!}{9! \cdot 5!} \cdot 2^5 =\\ \displaystyle = \frac{ 240.240 }{ 120 } \cdot 2^5 = 2002 \cdot 32 = 64.064

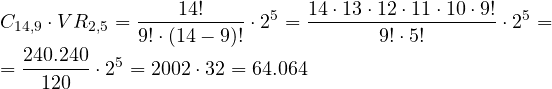
Este ejercicio es una combinación de los dos anteriores.

Deja un comentario