Variaciones con repetición: Introducción

 

Las variaciones con repetición de n elementos tomados de r en r (de orden r) son los grupos iguales o distintos de r elementos que se pueden formar con los n elementos que tenemos.

De esta forma dos grupos se diferencian porque:

  1. tienen algún elemento distinto, o
  2. porque tienen diferente orden de colocación.

Se representa por VR_{n,r} con \begin{cases}r<n\\r \geq n \end{cases}

 

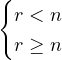
Para construir las variaciones con repetición, partimos de un conjunto A=\{1,2,3\} y elaboramos todas las variaciones con repetición posibles.

De un elemento: Si tenemos un conjunto de tres elementos y queremos hacer grupos de uno, únicamente podremos hacer tres grupos:

  • 1, 2, 3.

De dos elementos: Se pueden obtener a partir de las de orden uno, añadiendo el segundo elemento. Como se pueden repetir, el segundo elemento puede ser el original y cualquiera de los dos restantes.

Así se obtienen los pares:

  • 11, 12, 13
  • 21, 22, 23
  • 31, 32, 33

De tres elementos. Las obtenemos a partir de las anteriores, añadiendo a cada una de ellas los dos elementos que faltan.

Se obtienen las siguientes ternas:

  • 111, 112, 113, 121, 122, 123, 131, 132, 133
  • 211, 212, 213, 221, 222, 223, 231, 232, 233
  • 311, 312, 313, 321, 322, 323, 331, 332, 333

Entonces, ¿cuántas variaciones hay?

Siguiendo la construcción ordenada que se ha realizado, es fácil deducir una fórmula para obtener el número de variaciones ordinarias o sin repetición:

  • De orden uno: VR_{3,1}=3^1=3.
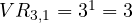  • De orden dos: VR_{3,2}=3^2=9.
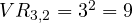  • De orden tres: VR_{3,3}=3^3=27.

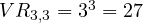A partir de estos desarrollos es fácil observar que para calcular el número de variaciones con repetición VR_{n,r} se realiza una potencia.

Es decir, la fórmula final es la siguiente:

    \[VR_{n,r}=n^r\]

 

Ejemplos

¿Cuántos resultados hay al lanzar una moneda al aire 6 veces? ¿Y si se lanza un dado dos veces?

Moneda: ROE – n = 2, r = 6

VR_{2,6}=2^6=64

Dado: ROE – n = 6, r = 2

VR_{6,2}=6^2=36 \smallskip

¿Cuántos números de 5 cifras se pueden formar con los dígitos 1, 2 y 3?

ROE – n = 3, r = 5

VR_{3,5}=3^5=243 \smallskip

¿Cuántos números de 3 cifras se pueden formar con los dígitos 1, 2, 3, 4 y 5?

ROE – n = 5, r = 3

VR_{5,3}=5^3=125 \smallskip

¿Cuántos números de 3 cifras se pueden formar con los dígitos 1, 2 y 3?

ROE – n = 3, r = 3

VR_{3,3}=3^3=27

 

¿Cómo se diferencia en los problemas la ‘n’ de la ‘r’?

Como se puede comprobar en los ejemplos, a diferencia de las variaciones sin repetición, no es en absoluto trivial la diferencia entre la n y la r. Hay que ir con mucho cuidado.

En los casos de la moneda y el dado, son dos tipos de problemas que no se pueden hacer con variaciones sin repetición, a no ser que se especifique en el enunciado que en los posibles casos debe excluirse la repetición.

Por ejemplo, si se tiran dos dados y se pregunta cuántos números de dos cifras pueden salir, el resultado es 36:

11, 12, 13, 14, 15, 16, 21, 22, 23, 24, 25, 26,

31, 32, 33, 34, 35, 36, 41, 42, 43, 44, 45, 46

51, 52, 53, 54, 55, 56, 61, 62, 63, 64, 65, 66

Pero si en el enunciado se impone que no pueden haber repeticiones, el resultado es 30, pues hay 6 repeticiones: 11, 22, 33, 44, 55 y 66. Entonces, ¿qué fómula de las variaciones funciona? En el primer caso la de variaciones con repetición y en el segundo la de variaciones sin repetición:

    \[ VR_{6,2}=6^2=36 \]

    \[ V_{6,2}=\frac{6!}{(6-2)!}=\frac{6\cdot5\cdot4!}{4!}=30 \]

Pero ¿qué sucede si en lugar de lanzarse 2 dados se tiran 6 monedas? El problema cambia radicalmente, porque en este caso n < r y por lo tanto en las variaciones sin repetición el denominador quedaría negativo:

    \[ V_{2,6}=\frac{2!}{(2-6)!}=\frac{2!}{(-4)!} \]

¿Qué quiere decir esto? Veámoslo. Las posibles opciones que pueden salir son:

    \[ VR_{2,6}=2^6=64 \]

¿Alguna de ellas tiene el espacio muestral con elementos que no se repitan? No, eso es imposible. Porque solo hay dos opciones (cara y cruz) que necesariamente deben salir 6 veces (tantas como monedas) y por lo tanto siempre terminan repitiéndose caras y cruces. Por eso en la fórmula de las variaciones sin repetición sale un absurdo, pues es imposible un factorial negativo por definición.

Finalmente, en los problemas relacionados con los números, la n es el número de dígitos que intervienen. Por lo que respecta a la otra letra, cuando se trataba de variaciones sin repetición, siempre resultaba n > r. Esta afirmación se puede comprobar en los ejercicios que ya se han visto (VSR de números). Pero cuando interviene la repetición, hay que ir con cuidado porque pueden darse los tres casos siguientes, como ya hemos visto en los ejemplos superiores:

    \[ \begin{cases}r<n\\ r=n \\r>n \end{cases} \]

Para poder comprender mejor estos conceptos se verán más ejercicios relacionados con sorteos, premios, códigos y palabras. De momento, en el siguiente vídeo se repasa lo explicado más algunos de los ejercicios.

 

 

Deja un comentario