ROE – n = 4, r = 3
![]()
ROE – n = 3, r = 4
![]()
ROE – n = 6, r = 3
![]()
En un principio se trata de ![]() .
.
Pero hay que tener en cuenta tres casos:
- Se deben restar los números que empizan con cero, en cuyo caso tienen realmente dos dígitos.
- Después los que además tienen el cero como segundo número, pues se trata de variaciones con repetición y puede darse el caso de ser un número como el 003.
- Y finalmente el caso de que sea el número 000.
Es decir:
![]()
Nota: Es importante comparar este ejercicio con otro semejante que se había visto en el caso de variaciones sin repetición. Como el número cero solo podía salir una vez, no se debían restar las opciones en las que apareciera además en el resto de posiciones. Pero como ahora sí que hay repetición, debe restarse en todas las posiciones.
ROE – n =9, r = 4
![]()
ROE – n = 9, r = 4
![]()
El número será de la forma X _ _ X, variando solo dos elementos intermedios sin repetición ![]() y con X tomando los valores del 1 al 9 para cada bloque de variaciones. Es decir:
y con X tomando los valores del 1 al 9 para cada bloque de variaciones. Es decir:
![]()
El número será de la forma X _ _ X, variando solo dos elementos intermedios con repetición ![]() y con X tomando los valores del 1 al 9 para cada bloque de variaciones. Es decir:
y con X tomando los valores del 1 al 9 para cada bloque de variaciones. Es decir:
![]()
ROE – n = 3, r = 6
![]()
En primer lugar se contabilizan todas las posibilidades:
ROE – n = 3, r = 6
![]()
A continuación se deben restar los siguientes dos posibles casos:
- Cuando falta uno de los tres dígitos (hay tres posibilidades, que falte el 1, el 2 o el 3):
ROE – n = 2, r = 6
![]()
- Cuando faltan dos de los tres dígitos solo pueden darse estas tres posibilidades:
111111 (faltan el 2 y el 3)
222222 (faltan el 1 y el 3)
333333 (faltan el 1 y el 2)
Por lo tanto, el resultado es:
![]()
Un número capicúa de 5 cifras tiene la forma ABCBA. Por lo tanto, basta con calcular las posibles ordenaciones relacionadas con los tres primeros números ABC o con los tres últimos CBA. Es decir, importa el orden y además no queda otra opción que repetir los dígitos por ser un número capicúa. Pero aunque parezca lo contrario no entran todos los elementos, precisamente por el hecho de seleccionarse solo la mitad por la repetición. Por lo tanto:
![]()
Un número capicúa de 6 cifras tiene la forma ABCCBA. Por lo tanto, en un pricipio debería bastar con calcular las posibles ordenaciones relacionadas con los tres primeros números ABC. Es decir, importa el orden y además se pueden repetir los dígitos. Por lo tanto, en un principio:
![]()
Pero resulta que los números que comienzan por cero no son capicúas. Por ejmplo, el número 012210 es realmente el 12210 y en efecto no es capicúa. Luego se tienen que restar los que comienzan por cero. Es decir:
![]()
¿Hemos terminado? Tal vez no. Porque como puede haber repetición, el cero se puede repetir saliendo un número de la forma 00XX00, que evidentemente no es capicúa porque se trata realmente del número XX00. Luego se tienen que restar los que además de comenzar por cero tienen otro cero en la segunda posición. Es decir:
![]()
Y ahora, ¿se puede decir que hemos terminado? Casi, pero todavía no. Nuevamente, como se puede repetir el número cero, queda un último número que es el que tiene también un cero en la tercera posición. Es decir, el de la forma 000000. Y este tampoco es capicúa, evidentemente. Por lo tanto:
![]()
Ya hemos terminado: Hay 889 números capicúas de 6 cifras.
Como el número es capicúa de 6 cifras, termina en par y además es distinto de cero, basta con fijarse en la primera mitad que además será de la forma PAR _ _.
Al haber 4 cifras pares fijadas de antemano:
![]()
Este ejercicio es una mezcla de los dos anteriores, pues son múltiplos de 5 los que terminan en 0 y 5. Pero al ser capicúa basta con fijarse en las tres primeras cifras del número.
Por un lado, al imponerse esta condición los números empezarán de la forma 5 _ _ o también 0 _ _.
En el primer caso:
![]()
Pero como además pueden comenzar por 0 _ _ , 0 0 _ y 0 0 0, entonces:
![]()
Así que hay ![]() números capicúas múltiplos de 5.
números capicúas múltiplos de 5.
Al ser capicúa, nuevamente debemos fijarnos solo en los tres primeros dígitos.
En la primera posición hay solo dos posibilidades: que comiencen por 1 y 2. Pues ya hemos visto que por cero no puede empezar.
En la segunda posición existen ![]() posibilidades. Pero nuevamente debemos restar los casos con ceros al comienzo.
posibilidades. Pero nuevamente debemos restar los casos con ceros al comienzo.
Por lo tanto:
![]()
Primero hay que calcular cuántos números hay, teniendo en cuenta que a diferencia del mismo ejercicio en las variaciones sin repetición ahora sí que puede producirse repetición porque no se informa que deban ser números ‘distintos’. De esta forma:
![]()
Ahora vamos a la suma.
Como ya se ha visto en ese ejercicio, el número es de 3 cifras y por lo tanto tiene tres posiciones: unidades, decenas y centenas.
Además, como hay 4 números, cada uno de ellos puede aparecer 64/4 = 16 veces en cada posición.
Por lo tanto, en las unidades:
- El 2 →
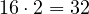
- El 4 →
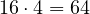
- El 6 →
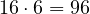
- El 8 →
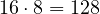
La suma de las unidades es: ![]()
La suma de las decenas: ![]()
La suma de las centenas: ![]()
Finalmente, la suma total es: ![]()
