Variaciones sin repetición: Introducción

 

Las variaciones sin repetición de n elementos tomados de r en r (de orden r) son los grupos distintos de r elementos que se pueden formar con los n elementos que tenemos.

De esta forma dos grupos se diferencian porque:

  1. tienen algún elemento distinto,
  2. o porque tienen diferente orden de colocación.

Se representa por V_{n,r} con r<n

 

Para construir las variaciones sin repetición, partimos de un conjunto A=\{1,2,3,4\} y elaboramos todas las variaciones sin repetición posibles.

De un elemento: Si tenemos un conjunto de cuatro elementos y queremos hacer grupos de uno, únicamente podremos hacer cuatro grupos:

  • 1, 2, 3, 4.

De dos elementos: Se pueden obtener a partir de las de orden uno, añadiendo el segundo elemento. Como no se pueden repetir, el segundo elemento puede ser cualquiera de los tres restantes.

Así se obtienen los pares:

  • 12, 13, 14,
  • 21, 23, 24,
  • 31, 32, 34,
  • 41, 42, 43.

De tres elementos. Las obtenemos a partir de las anteriores, añadiendo a cada una de ellas los dos elementos que faltan.

Se obtienen las siguientes ternas:

  • 123, 124, 132, 134, 142, 143,
  • 213, 214, 231, 234, 241, 243,
  • 312, 314, 321, 324, 341, 342,
  • 412, 413, 421, 423, 431, 432.

De cuatro elementos. Se obtienen a partir de las de orden tres, añadiendo a cada una de ellas el elemento que falta.

Los números son:

  • 1234, 1243, 1324, 1342, 1423, 1432,
  • 2134, 2143, 2314, 2341, 2413, 2431,
  • 3124, 3142, 3214, 3241, 3412, 3421,
  • 4123, 4132, 4213, 4231, 4312, 4321.

Como estamos construyendo variaciones sin repetición y los elementos no se pueden repetir, ya no podemos continuar construyendo variaciones de orden cinco.

Entonces, ¿cuántas variaciones hay?

Siguiendo la construcción ordenada que se ha realizado, es fácil deducir una fórmula para obtener el número de variaciones ordinarias o sin repetición:

  • De orden uno: Hay cuatro. V_{4,1}=4.
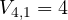  • De orden dos: Añadiendo tres elementos a cada una de las anteriores. V_{4,2}=4 \cdot 3=12.
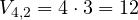  • De orden tres. Añadiendo dos elementos a cada una de las anteriores. V_{4,3}=4 \cdot 3 \cdot 2=24.
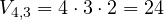  • De orden cuatro. Añadido un elemento al anterior. V_{4,4}=4 \cdot 3 \cdot 2 \cdot 1=24.

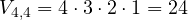A partir de estos desarrollos es fácil observar que para calcular el número de variaciones sin repetición V_{n,r}se realiza un producto de factores consecutivos en orden decreciente empezando por n y colocando un número de factores igual a r.

Es decir, la fórmula final es la siguiente:

    \[V{n,r}={n!\over(n-r)!}\]

 

Ejemplos

¿Cuántos números de 4 cifras distintas se pueden formar con los dígitos del 1 al 9?

ROE – n = 9, r = 4

\displaystyle V_{9,4}=\frac{9!}{(9-4)!}=\frac{9!}{5!}=\frac{9\cdot8\cdot7\cdot6\cdot5!}{5!}=3.024 \smallskip

En una carrera de 100 metros participan 8 corredores. ¿De cuántas maneras diferentes se podrán repartir las medallas de oro, plata y bronce?

ROE – n = 8, r = 3

\displaystyle V_{8,3}=\frac{8!}{(8-3)!}=\frac{8!}{5!}=\frac{8\cdot7\cdot6\cdot5!}{5!}=336

 

En el siguiente vídeo se repasan estos conceptos y se explican algunos de los próximos ejercicios.

Deja un comentario