Combinaciones: Número combinatorio - FIAR

El número $C_{n,r}$ de combinaciones ordinarias de $n$ elementos, tomados de $r$ en $r$ , se llama número combinatorio o coeficiente binómico y se representa mediante la expresión ${n \choose r}$ , que se lee $n$ sobre $r$ , siendo $n$ y $r$ números naturales.

$\displaystyle C_{n,r} = {n \choose r} = \frac {n!}{r!(n-r)!} = \frac {n-r+1}{r!}$

Propiedades

Como $0! = 1$ , el valor del número combinatorio es 1 cuando $r = 0$ o $r = n$ . Es decir:

${n \choose 0} = {n \choose n} = 1$

Demostración

$\displaystyle \left(\begin{array}{l}n \\ 0\end{array}\right)=\frac{n !}{0 !(n-0) !}=\frac{n !}{1 \cdot n !}=1 \smallskip$
$\displaystyle \left(\begin{array}{l}n \\ n\end{array}\right)=\frac{n !}{n !(n-n) !}=\frac{n !}{n ! 0 !}=\frac{1}{1}=1$

Cualquier número natural $n$ puede expresarse como el número combinatorio de $n$ sobre 1. Es decir:

${n \choose 1} = n$

Demostración

$\displaystyle \left(\begin{array}{l}n \\ 1\end{array}\right)=\frac{n!}{1!(n-1)!}=\frac{n(n-1)!}{1(n-1)!}=n$

Dos números combinatorios son iguales si sus índices superiores son iguales y la suma de los inferiores es igual al índice superior:

${n \choose r} = {n \choose n-r}$

Demostración
Basta con comprobar que son iguales los desarrollos de los dos miembros de la igualdad anterior:

$\displaystyle {n \choose r} = \frac{n!}{r!(n-r)!}$

$\displaystyle {n \choose n-r} = \frac{n!}{(n-r)![n-(n-r)]!} = \frac{n!}{(n-r)!(n-n+r)!} = \frac{n!}{r!(n-r)!} \smallskip$

Ejemplos

$\displaystyle C_{10,6}=C_{10,4} \smallskip$
$\displaystyle {12 \choose 5} = {12 \choose 7} \smallskip$
$\displaystyle {100 \choose 98} = {100 \choose 2} \smallskip$
$\displaystyle {x \choose x-3} = {x \choose 3} \smallskip$

EJERCICIOS 1

Ejercicios resueltos

$\displaystyle {x \choose 7} = {x \choose 3} ;\enspace x-7=3 ;\enspace x=10 \smallskip$
$\displaystyle {x \choose 4} = {x \choose 9} ;\enspace x-4=9 ;\enspace x=13 \smallskip$
$\displaystyle {x+1 \choose 5} = {x+1 \choose 6} ;\enspace x+1-5=6 ;\enspace x-4=6 ;\enspace x=10 \smallskip$
$\displaystyle {39 \choose x} = {39 \choose x+5} ;\enspace 39-x=x+5 ;\enspace 39-5=2x ;\enspace 34=2x ;\enspace x=17 \smallskip$

EJERCICIOS 2

La suma de dos números combinatorios cuyos índices superiores son iguales y los inferiores difieren es una unidad, es igual a otro número combinatorio con índice superior sumado en una unidad e índice inferior el mayor de los dos:

${n \choose r} + {n \choose r+1} = {n+1 \choose r+1}$

Demostración

$\displaystyle \left(\begin{array}{l}n \\ r\end{array}\right)=\frac{n!}{r!(n-r)!} \smallskip$
$\displaystyle \left(\begin{array}{c}n \\ r+1\end{array}\right)=\frac{n!}{(r+1)!(n-r-1)!} \smallskip$
$\displaystyle \left(\begin{array}{c}n+1 \\ r+1\end{array}\right) = \frac{(n+1)!}{(r+1)!(n-r)!} \smallskip$

$\displaystyle \left(\begin{array}{c}n \\ r\end{array}\right)+\left(\begin{array}{c}n \\ r+1\end{array}\right)=\frac{n!}{r!(n-r)!}+\frac{n!}{(r+1)!(n-r-1)!}= \smallskip$
$\displaystyle =\frac{n!}{r!(n-r)(n-r-1)!}+\frac{n!}{(r+1) r!(n-r-1)!}=\frac{n!}{r!(n-r-1)!}\left(\frac{1}{n-r}+\frac{1}{r+1}\right)= \smallskip$
$\displaystyle =\frac{n!}{r!(n-r-1)!} \cdot \frac{r+1+n-r}{(r+1)(n-r)}=\frac{(n+1)!}{(r+1)!(n-r)!}=\left(\begin{array}{l}n+1 \\ r+1\end{array}\right) \smallskip$

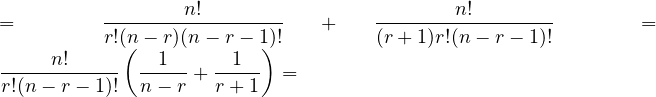
Ejemplos

$\displaystyle {8 \choose 4} + {8 \choose 5} = {9 \choose 5} \smallskip$
$\displaystyle {10 \choose 5} + {10 \choose 6} = {11 \choose 6} \smallskip$
$\displaystyle {x \choose 4} + {x \choose 5} = {x+1 \choose 5} \smallskip$
$\displaystyle {12 \choose x} + {12 \choose x+1} = {13 \choose x+1} \smallskip$

Ejercicios resueltos

$\displaystyle {x \choose 3} + {x \choose 4} = {9 \choose 4} ;\enspace {x+1 \choose 4} = {9 \choose 4} ;\enspace x+1-4=4 ;\enspace x=7 \smallskip$
$\displaystyle {x+1 \choose 7} + {x+1 \choose 6} = {11 \choose 7} ;\enspace {x+2 \choose 7} = {11 \choose 7} ;\enspace x+2-7=11 ;\enspace x=16 \smallskip$
$\displaystyle {9 \choose x-1} + {9 \choose x} = {10 \choose 7} ;\enspace {10 \choose x} = {10 \choose 7} ;\enspace 10-x=7 ;\enspace x=3 \smallskip$

EJERCICIOS 3

Más ejercicios resueltos

$\displaystyle \left(\begin{array}{l}x \\ 3\end{array}\right)=x-2 \smallskip$
$\displaystyle \frac{x!}{3!(x-3)!}=x-2 ;\enspace \frac{x(x-1)(x-2)(x-3)!}{3!(x-3)!}=x-2 \smallskip$
$\displaystyle x(x-1)=6 ;\enspace x^{2}-x-6=0 \smallskip$
$\displaystyle x_{1}=-2, x_{2}=3 \medskip$

$\displaystyle \left(\begin{array}{l}x \\ 5\end{array}\right)=\frac{2}{3}\left(\begin{array}{l}x \\ 6\end{array}\right) \smallskip$
$\displaystyle \frac{x!}{5!(x-5)!}=\frac{2}{3} \cdot \frac{x!}{6!(x-6)!} ;\enspace \frac{1}{(x-5)!}=\frac{2}{3} \cdot \frac{1}{6(x-6)!} \smallskip$
$\displaystyle (x-5)!=9(x-6)! ;\enspace (x-5)(x-6)!=9(x-6)! ;\enspace x-5=9 ;\enspace x=14 \medskip$

$\displaystyle 18\left(\begin{array}{c}x \\ 2\end{array}\right)+24\left(\begin{array}{c}x \\ 3\end{array}\right)=125x \smallskip$
$\displaystyle \frac{18x!}{2!(x-2)!}+\frac{24x!}{3!(x-3)!}=125x \smallskip$
$\displaystyle \frac{18 x (x-1) (x-2)!}{2!(x-2)!}+\frac{24 x(x-1)(x-2)(x-3)!}{3 !(x-3)!}=125x \smallskip$
$\displaystyle \frac{18(x-1)}{2}+\frac{24(x-1)(x-2)}{6}=125 ;\enspace 54(x-1)+24(x-1)(x-2)=750 \smallskip$
$\displaystyle 54 x-54+24 x^{2}-72 x+48=750 ;\enspace 24 x^{2}-18 x-756=0 \smallskip$
$\displaystyle x_{1}=-5.25, x_{2}=6 \medskip$

$\displaystyle 2\left(\begin{array}{c}x \\ 4\end{array}\right)=2\left(\begin{array}{c}x \\ 3\end{array}\right)-\left(\begin{array}{l}x \\ 2\end{array}\right) \smallskip$
$\displaystyle \frac{2 x!}{4!(x-4)!}=\frac{2x!}{3!(x-3)!}-\frac{x!}{2!(x-2)!} \smallskip$
$\displaystyle \frac{2}{4!(x-4)!}=\frac{2}{3!(x-3)(x-4)!}-\frac{1}{2!(x-2)(x-3)(x-4)!} \smallskip$
$\displaystyle \frac{2}{4!}=\frac{2}{3!(x-3)}-\frac{1}{2!(x-2)(x-3)} ;\enspace \frac{1}{4 \cdot 3}=\frac{1}{3(x-3)}-\frac{1}{2(x-2)(x-3)} \smallskip$
$\displaystyle \frac{(x-2)(x-3)}{12(x-2)(x-3)}=\frac{4(x-2)}{12(x-2)(x-3)}-\frac{6}{12(x-2)(x-3)} \smallskip$
$\displaystyle (x-2)(x-3)=4(x-2)-6 ;\enspace x^{2}-5 x+6=4 x-8-6\smallskip$
$\displaystyle x^{2}-5 x-4 x+6+8+6=0 ;\enspace x^{2}-9 x+20=0\smallskip$
$\displaystyle x_{1}=4 ;\enspace x_{2}=5\medskip$

EJERCICIOS 4

Propiedades

Deja un comentarioCancelar respuesta