Q1. ¿Cuántas opciones hay, si se deben escoger tres asignaturas entre seis optativas?
ROE – n = 6, r = 3
![\[ C_{6,3} = \frac{6!}{3! \cdot (6-3)!} = \frac{6 \cdot 5 \cdot 4 \cdot 3!}{3! \cdot 3!} = \frac{5 \cdot 4}{1} = 20 \]](https://kid.fiar.me/wp-content/ql-cache/quicklatex.com-fa63da0ae517af3fa31ba36f21a165a6_l3.png "Rendered by QuickLaTeX.com")
Q2. Se quiere preparar una salsa con 3 ingredientes y tenemos 7 en la nevera. ¿Cuántos tipos de salsa se puede hacer?
ROE – n = 7 , r = 3
![\[ C_{7,3} = \frac{7!}{3! \cdot (7-3)!} = \frac{7 \cdot 6 \cdot 5 \cdot 4!}{3! \cdot 4!} = \frac{7 \cdot 5}{1} = 35 \]](https://kid.fiar.me/wp-content/ql-cache/quicklatex.com-c9dbd0eac038d1d9007a13f5f85d94df_l3.png "Rendered by QuickLaTeX.com")
Q3. En un programa de TV hay 4 presentadores. Si la plantilla es de 10 periodistas, ¿de cuántas formas se puede presentar el programa?
ROE – n = 10, r = 4
![\[ C_{10,4} = \frac{10!}{4! \cdot (10-4)!} = \frac{10 \cdot 9 \cdot 8 \cdot 7 \cdot 6!}{4! \cdot 6!} = \frac{5040}{24} = 210 \]](https://kid.fiar.me/wp-content/ql-cache/quicklatex.com-7b2cbcc3dd9d9e5ce7ba3623fbd3b1dc_l3.png "Rendered by QuickLaTeX.com")
Q4. Se ofrecen seis discos para dos regalos. ¿Cuántas posibilidades hay si los regalos son distintos y diferentes?
ROE – n = 6, r = 2
![\[ C_{6,2} = \frac{6!}{2! \cdot (6-2)!} = \frac{6 \cdot 5 \cdot 4!}{2! \cdot 4!} = \frac{30}{2} = 15 \]](https://kid.fiar.me/wp-content/ql-cache/quicklatex.com-dc7e5877dc73fa47ac8e48ff26e65e08_l3.png "Rendered by QuickLaTeX.com")
Q5. Se distribuyen 5 regalos distintos entre tres personas. ¿De cuántas formas se pueden repartir si estos regalos son iguales?
ROE – n = 5, r = 3
![\[ C_{5,3} = \frac{5!}{3! \cdot (5-3)!} = \frac{5 \cdot 4 \cdot 3 \cdot 2!}{3! \cdot 2!} = \frac{60}{6} = 10 \]](https://kid.fiar.me/wp-content/ql-cache/quicklatex.com-7f39475a5861425b269c251c5e46e26b_l3.png "Rendered by QuickLaTeX.com")
Q6. Se distribuyen 5 regalos distintos entre tres personas. ¿De cuántas formas se pueden repartir si estos regalos son distintos?
ROE – n = 5, r = 3
![\[ V_{5,3} = \frac{5!}{(5-3)!} = \frac{5 \cdot 4 \cdot 3 \cdot 2!}{2!} = 60 \]](https://kid.fiar.me/wp-content/ql-cache/quicklatex.com-66f360712079b1e2c5a421d094222036_l3.png "Rendered by QuickLaTeX.com")
Este ejemplo es útil para entender la diferencia entre las combinaciones y las variaciones: la importancia del orden. En este caso se trata de la diferencia entre ser o no los regalos iguales.
Q7. A una reunión asisten 15 personas y se intercambian saludos entre todos. ¿Cuántos saludos se han intercambiado?
ROE – n = 15, r = 2
![\[ C_{15,2} = \frac{15!}{2! \cdot (15-2)!} = \frac{15 \cdot 14 \cdot 13!}{2! \cdot 13!} = \frac{210}{2} = 105 \]](https://kid.fiar.me/wp-content/ql-cache/quicklatex.com-87673f7b0e12f1292c056005200ca971_l3.png "Rendered by QuickLaTeX.com")
Q8. ¿Cuántos grupos de 5 alumnos podemos formar con los 30 alumnos de una clase, suponiendo que un grupo se diferencia del otro al menos en un alumno?
ROE – n = 30, r = 5
Que se diferencien «al menos en un alumno», quiere decir que los grupos son distintos por las personas que los componen y no por el orden que ocupan.
![\[ C_{30,5} = \frac{30!}{5! \cdot (30-5)!} = \frac{30 \cdot 29 \cdot 28 \cdot 27 \cdot 26 \cdot 25!}{5! \cdot 25!} = \frac{17100720}{120} = 142.506 \]](https://kid.fiar.me/wp-content/ql-cache/quicklatex.com-af3b2f07540fe064e5a6dce7c7c1b611_l3.png "Rendered by QuickLaTeX.com")
Q9. En una clase hay 10 niños y 6 niñas. ¿De cuántas maneras se puede hacer un grupo de 3 alumnos?
ROE – n = 16, r = 3
![\[ C_{16,3} = \frac{16!}{3! \cdot (16-3)!} = \frac{16 \cdot 15 \cdot 14 \cdot 13!}{3! \cdot 12!} = \frac{3360}{6} = 560 \]](https://kid.fiar.me/wp-content/ql-cache/quicklatex.com-7b713c3cd973477551563d6e746af7d1_l3.png "Rendered by QuickLaTeX.com")
Q10. En una clase hay 10 niños y 6 niñas. ¿De cuántas maneras se pueden seleccionar 3 niños?
ROE – n = 10, r = 3
![\[ C_{10,3} = \frac{10!}{3! \cdot (10-3)!} = \frac{10 \cdot 9 \cdot 8 \cdot 7!}{3! \cdot 7!} = \frac{720}{6} = 120 \]](https://kid.fiar.me/wp-content/ql-cache/quicklatex.com-e94ecb84623e7767b146ecb9d412bbe7_l3.png "Rendered by QuickLaTeX.com")
Q11. En una clase hay 10 niños y 6 niñas. ¿De cuántas maneras se pueden seleccionar 2 niños y una niña?
![\[ C_{10,2} = \frac{10!}{2! \cdot (10-2)!} = \frac{10 \cdot 9 \cdot 8!}{2! \cdot 8!} = \frac{90}{2} = 45 \]](https://kid.fiar.me/wp-content/ql-cache/quicklatex.com-51346bc61be9b658b9f79e54399ecdcb_l3.png "Rendered by QuickLaTeX.com")
![\[ C_{6,1} = \frac{6!}{1! \cdot (6-1)!} = \frac{6 \cdot 5!}{1! \cdot 5!} = \frac{6}{1} = 6 \]](https://kid.fiar.me/wp-content/ql-cache/quicklatex.com-a5df7715982e095f0e6499bd873e60d6_l3.png "Rendered by QuickLaTeX.com")
La probabilidad de seleccionar dos niños y una niña es: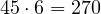 
Q12. En una clase hay 10 niños y 6 niñas. ¿De cuántas maneras se puede seleccionar al menos un niño?
La posibilidad de seleccionar como mínimo un niño es el suceso contrario de seleccionar tres niñas y ningún niño:
![\[ C_{6,3} = \frac{6!}{3! \cdot (6-3)!} = \frac{6 \cdot 5 \cdot 4 \cdot 3!}{3! \cdot 3!} = \frac{120}{6} = 20 \]](https://kid.fiar.me/wp-content/ql-cache/quicklatex.com-10235e8dcfc45fe74aa2615a54acb1f4_l3.png "Rendered by QuickLaTeX.com")
Como la posibilidad de seleccionar 3 (con independencia de si son niños o niñas) es de 560 y la de que solo sean niñas es de 20, el conjunto de sucesos en el que al menos hay un niño es de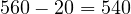 
Q13. ¿De cuántas maneras se pueden distribuir las 8 últimas butacas de un partido de fútbol entre los 12 aficionados que están haciendo cola?
ROE – n = 12, r = 8
![\[ C_{12,8} = \frac{12!}{8! \cdot (12-8)!} = \frac{12 \cdot 11 \cdot 10 \cdot 9 \cdot 8 \cdot 7 \cdot 6 \cdot 5 \cdot 4!}{8! \cdot 4!} = \frac{19958400}{40320} = 495 \]](https://kid.fiar.me/wp-content/ql-cache/quicklatex.com-4615463266f062ca217db18adc0b01e2_l3.png "Rendered by QuickLaTeX.com")
